Structure in Unstructured Data, Part 2

Follow this link for an updated post.

In the first part, we took a random walk from unstructured data to multimedia files, JPEG compression, a DCT-inspired classifier, and deep learning. We saw that the crux of supervised machine learning is the training.

There are two reasons for needing classifiers. We can design more precise algorithms if we can specialize them for a certain data class. For humans, the reason is that our immediate memory can hold only 7±2 chunks of information. This means that we aim to break down information into categories each holding 7±2 chunks. There is no way humans can interpret the graphical representation of graphs with billions of nodes.

As already Immanuel Kant noted, categories are not natural or genetic entities, they are purely the product of acquired knowledge. One of the functions of the school system is to create a common cultural background, so people learn to categorize according to similar rules and understand each other's classifications. For example, in the biology class, we learn to organize botany according to the 1735 Systema Naturæ compiled by Carl Linnæus.

As we know from Jean Piaget's epistemological studies with children, there is assimilation when a child responds to a new event in a way that is consistent with an existing classification schema. There is accommodation when a child either modifies an existing schema or forms an entirely new schema to deal with a new object or event. Piaget conceived intellectual development as an upward expanding spiral in which children must constantly reconstruct the ideas formed at earlier levels with new, higher order concepts acquired at the next level.

The data scientist's social role is to further expand this spiral.

For data, this means that we want to cluster it (recoding by categorization). Further, we want to connect the clusters in a graph so we can understand its structure (finding patterns). At first, clustering looks easy: we take the training set and do a Delaunay triangulation, the dual graph of the Voronoi diagram. After building the graph with the training set, for a new data point, we just look in which triangle it falls and know its category. Color scientists are familiar with Delaunay triangulations because they are used for device modeling by table lookup. Engineers use them to build meshes for finite element methods.

The problem is that the data is statistical. There is no clear-cut triangulation and points from one category can lie in a nearby category with a certain probability. Roughly, we build clusters by taking neighborhoods around the points and the intersect them to form the clusters. The crux is to know what radius to pick for the neighborhoods because the result will be very different.

This is where the relatively new field of algebraic topology analytics comes into play. It has only been about 15 years that topology has started looking at point clouds. Topology, an idea of the Swiss mathematician Leonhard Euler, studies the properties of shape independent of coordinate systems, dependent only on a metric. The topological properties are deformation invariant (a donut is topologically equivalent to a mug). Finally, topology constructs compressed representations of shape.

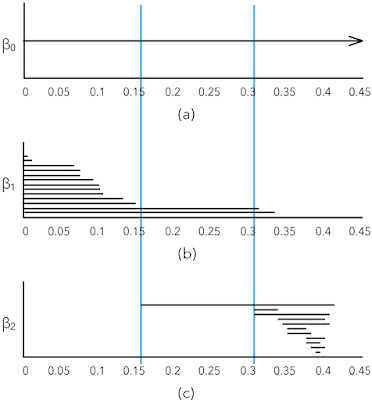
The interesting element of shape in point clouds are the k-th Betti numbers β_k, the number of k-dimensional "holes" in a simplicial complex. For example, informally β₀ is the number of connected components, β₁ the number of roundish holes, and β₂ the number of cavities.

Algebraic topology analytics relieves the data scientist from having to guess the correct radius of the point neighborhoods by considering all radii and retaining only those that change the topology. If you want to visualize this idea, you can think of a dendrogram. You start with all the points and represent them as leaves; as the radii increase, you walk up the hierarchy in the dendrogram.

This solves the issue of having to guess a good radius to form the clusters, but you still have the crux of having to find the most suitable distance metric for your data set. This framework is not a dumb black-box: you still need the skills and experience of a data scientist.

The dendrogram is not sufficiently powerful to describe the shape of point clouds. The better tool is the set of k-dimensional persistence barcodes that show the Betti numbers in function of the neighborhood radii for building the simplicial complexes. Here is an example from page 347 in Carlsson's article cited below:

With large data sets, when we have a graph, we do not necessarily have something we can look at because there is too much information. Often we have small patterns or motifs and we want to study how a higher order graph is captured by a motif. This is also a clustering framework.

For example, we can look at the Stanford web graph at some time in 2002 when there were 281,903 nodes (pages) and 2,312,497 edges (links).

We want to find the core group of nodes with many incoming links and the tied together periphery groups that are tied together and also up-link to the core.

A motif that works well for social network kind of data is that of three interlinked nodes. Here are the motifs with three nodes and three edges:

In motif M₇ we marked the top node in red to match the figure of the Stanford web.

Conceptually, given a higher order graph and a motif M_i, the framework searches for a cluster of nodes S with two goals:

1. the nodes in S should participate in many instances of M_i
2. the set S should avoid cutting instances of M_i, which occurs when only a subset of the nodes from a motif are in the set S

The mathematical basis for this framework are motif adjacency matrices and the motif Laplacian. With these tools, a conductance metric in spectral graph theory can be defined, which is minimized to find S. The third paper in the references below contains several worked through examples for those who want to understand the framework.

Further reading:

• G. A. Miller. The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63(2):81–97, 1956
• G. Carlsson. Topological pattern recognition for point cloud data. Acta Numerica, 23:289–368, 5 2014
• A. R. Benson, D. F. Gleich, and J. Leskovec. Higher-order organization of complex networks. Science, 353(6295):163–166, 2016