g2 camera calibration for RIPs

There has been quite a bit of speculation about the motivation behind our work on the g⁽²⁾ camera; we have even been slashdotted last January 25^th, so we might as well open the kimono on it, at least a little tiny bit.

In fact we are now well protected after getting the necessary patents. Every year, 15 days before Tax Day, viz. on April 1^st, the Patent Office allows inventors to demo their apparatus directly to the examiners, instead of filing a written patent application. Doing a demo is very efficient. We set up shop in the enormous hall of the Madison Building (see picture below, the tables outdoors are for inventors demonstrating a perpetuum mobile). We had two rows of tables with all the prototypes, gizmos, and gadgets we had developed and demonstrated them step by step and claim by claim to the attentive Examiners.

Of course the examiners had many questions and doubts, but fortunately at the left of the hall shown in the above picture there is one of the best libraries on this planet, so while we engineers were haggling with the Examiners, our managers and patent attorneys were busy building stronger cases and strengthening the claims.

Further down on Duke Street, on the block after the Whole Foods Market, there is a Marriott Residence Inn, where we could stay six people in each suite and get a lot of quality time to polish our inventions, while our interns prepared hearty meals for us. Our patent attorneys were comfortably lodging at the Westin across the street from the Federal Court building.

But, we are digressing — back to the motivation for the g⁽²⁾ camera. In high-speed digital printing, the bottleneck has always been in the ripping (RIP, Raster Image Processor) or, in HP parlance, the DFE (Digital Front End). For example, when we were working on the Xenith system at PARC in the mid-Eighties, Nick Sheridon was running the print engine at 300 ppm using Tibor Fisli's quad-spot laser diodes, while Gary Starkweather cranked the resolution up to 4000 dpi. Yet, even after adopting the Dragon's MBus, the shipping Docutech product could only run at 100 ppm and 600 dpi due to RIP limitations.

Concomitantly, at Canon the A-printer had been developed. This poster printer had a 40 inch wide array and was printing on paper rolls using bubble jet. The head actually consisted of four 10 inch heads mounted in a staggered pattern, and it was incredibly fast. Only, it required a MasPar mini-supercomputer to deliver the bits. The galleries and poster shops in Roppongi never ordered enough printers to make the product commercially viable.

Today, our valued customers buying high-speed digital presses still have to dive deep into their pockets to buy a costly DFE. This is why in Director Gary Dispoto's Print Production Automation Lab, Dr. I-Jong Lin manages the RIP project. This is also why Dr. Ray Beausoleil — who just became an HP Fellow — moved to the Quantum Science Research Department. We need quantum information technology (QIT) to deliver affordable DFEs for our high-speed digital presses.

One of the challenges in QIT is to store quantum bits (qbits) while avoiding a collapse of the wave function or decoherence. Typically, qbits are stored in a semiconductor (gallium arsenide, GaAs) microcavity, therefore, we have to study the interface interactions of emanating photons.

More formally, we need to study the Bose-Einstein condensation (BEC) phase transition in a polariton system in a semiconductor microcavity. The macroscopic quantum degeneracy is typically detected by probing the statistical properties of light emitted from a microcavity, under the presumption that the statistics of the exciton polaritons are faithfully transferred to the emanating photons.

The figure below shows Interference fringes (a) at 770 nm wavelength used to verify the BEC of polaritons in GaAs microcavity and (b) at 546 nm measured for the green line of a pulsed Hg-Ar discharge lamp.

This figure shows, that a coherent light source (e.g., a photon laser or decaying polariton BEC) can exhibit the same first-order correlations as a chaotic (or thermal) light source (e.g. Hg-Ar discharge lamp in (b)). The table below shows that proper disambiguation of a coherent state also requires measurement of the second-order correlation function g⁽²⁾ associated with intensity noise correlations:

Function	Incoherent	Coherent	Chaotic
g(1)	0	1	1
g(2)	1	1	2

In summary, as we wrote in our slashdotted paper, the application of the g⁽²⁾ camera is to take pictures to confirm the presence of true Bose–Einstein condensates (BEC). The next challenge is calibrating the camera. As we wrote in or popular technical report on Spectrophotometer Calibration and Certification, tight calibration is very critical in this kind of applications.

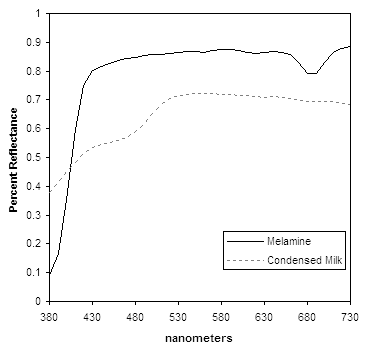
Fortunately, there is a condensate that is readily available and which is produced industrially at very tight tolerances: condensed milk. Alas, in our experiments we found a caveat. From the figure below we know that we are dealing with photon pairs. To correctly calibrate the SPADs, we have to be certain that both calibration photons have exactly the same color.

As our esteemed colleague and co-blogger Steve Simske keeps warning us about, the caveat is in the rampant counterfeiting happening in the supply chain. What happens if one photon comes from the condensed milk but the other photon comes from melamine?

In our lab we have built a special spectroradiometer, which we use as a reference for the calibration instrument. We have used it to measure the spectrum of pure condensed milk and that of melamine. Here are the plots:

Now we just use the CIE formula with the color matching functions for the 2º observer:

and get the RGB values of the two photons.

Color science is about observers, and in the end what counts is whether an observer can tell apart photons with these two RGB values. The old way of doing this was to compute the ∆E*_ab value in a perceptually uniform color space or in a CIECAM02 color appearance space based on the JND (just noticeable difference).

In our work on the color thesaurus we have established that a more reliable method is to determine whether the names of the two photon's colors are synonyms. Since the first to take a picture of a BEC will almost certainly get the Nobel Prize, we decided to use the data from our Swedish corpus of the färgbenämningsexperiment.

The RGB values calculated above yield mjölkaktig vit for the condensate and snövit for the melamine. Clearly there is no match and the g⁽²⁾ camera would be calibrated incorrectly if the condensate is counterfeited. How did we solve this problem? The solution is in this Feinman diagram:

Since photons are massless bosons, time is symmetric and at an event E we can say that a first photon (signal s) comes from a second photon (idler i) when the two photons are entangled to form a biphoton, In other words, each biphoton can be regarded as forming a loop between source and detector (CC is the coincidence counter).

Entanglement is just a fancy technical term to say that the two photon share the same wave function, also known as Schrödinger equation. Since the color of a photon is given by its wavelength, by entangling two photons we make them of the same color.

In other words, all we have to do, is to entangle the condensed milk photons with the melamine photons and we can always calibrate correctly the g⁽²⁾ camera, regardless of possible counterfeiting with melamine, because the photons get the same color.

This movie shows principal color scientist Nathan Moroney in our lab entangling the photons.

Of course, the stirring requires a lot of training, because the wave function can easily collapse, so do not try this at home!

For the viewpoint of our performance analyst, see his post in the Performance Agora.

For now, having tattooed on our tonsils to finish the new RIP, we are focusing on that. Once we have delivered product, our future research ideas include feeding the entangled condensed milk photons to Schrödinger's cat and take its pictures with the g⁽²⁾ camera. We will post our images here, so stay tuned!

In the meantime, we wish you a happy April Fool's Day.